前言：

《CS：APP》又名深入理解计算机系统，被称为计算机学习的圣经，假期总算有时间进行一个习的学，在阅读书籍，观看CMU网课的同时，也顺便完成了部分lab，不得不说lab很有挑战，对于相应章节知识的学习和理解具有很棒的作用，本篇为第二章内容的lab: DATA LAB的学习笔记，下附相关学习资料。

lab学习官网：CS:APP3e, Bryant and O’Hallaron (cmu.edu)

网课地址：【精校中英字幕】2015 CMU 15-213 CSAPP 深入理解计算机系统课程视频_哔哩哔哩_bilibili

参考资源和博客：《深入理解计算机系统》第三版的实验文件、解答与笔记 (github.com)

Data Lab笔记

本lab内容主要包括位运算，补码运算，浮点数等相关内容，完成lab需要实现函数功能，同时会限制使用op运算符的个数,因此增加了完成的难度，所有的实现都基于32位系统。

所有的函数实现都在bits.c中完成，可以使用./btest对实现函数的正确性进行检验。使用./dlc对完成函数的语法正确性和使用操作符的限制进行检验，使用./driver.pl对以上两项检验进行合并。

本次lab实现的函数为2017年版本，最新的版本为2019年版本，对很多实现函数要求进行了更新。

1.位操作

1.bitAnd

/* 
 * bitAnd - x&y using only ~ and | 
 *   Example: bitAnd(6, 5) = 4
 *   Legal ops: ~ |
 *   Max ops: 8
 *   Rating: 1
 */
int bitAnd(int x, int y) {
  return ~(~x|~y);
}

题目要求只使用~和|完成&，参考德摩根定律即可实现

2.getByte

/* 
 * getByte - Extract byte n from word x
 *   Bytes numbered from 0 (LSB) to 3 (MSB)
 *   Examples: getByte(0x12345678,1) = 0x56
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 6
 *   Rating: 2
 */
int getByte(int x, int n) {
 int a=(x>>(n<<3))&0xff;
 return a;
}

本题是从 x 中提取出第 i 个字节（i=0,1,2,3），方法就是将那个字节移位至最低位，然后用屏蔽码 0xff 提取就可以了

3.logicalShift

/* 
 * logicalShift - shift x to the right by n, using a logical shift
 *   Can assume that 0 <= n <= 31
 *   Examples: logicalShift(0x87654321,4) = 0x08765432
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 20
 *   Rating: 3 
 */
int logicalShift(int x, int n) {
  int mask=(1<<(32+~n))|((~(1<<31))>>n);
  return x>>n&mask;
}

本题需要实现逻辑右移，本身c语言自带的>>指的是算术右移，因此可以在算术右移的基础上对其进行改进。

本题做法的核心思路是构造一个掩码，掩码可以对右移后的数据进行更新使其满足题意。例如右移4位，我们构造的掩码即为0x0fffffff，为此我们可以先构造一个0x7fffffff，因为其符号位为0，将其算术右移对应的n位后就可以满足上述的条件，但由于其移动n位的掩码正好与我们需要的差一位，因此补充一个(1<<(31-n))的|即可构造最终的掩码。

4.bitCount

/*
 * bitCount - returns count of number of 1's in word
 *   Examples: bitCount(5) = 2, bitCount(7) = 3
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 40
 *   Rating: 4
 */
int bitCount(int x) {
  int mask1=0x55;
  int mask2=0x33;
  int mask3=0xf;
  int mask4=0xff;
  int mask5=0;
  int k=0;
  mask1=(mask1<<8)|mask1;
  mask1=(mask1<<16)|mask1;
// mask1=0x55555555   

  mask2=(mask2<<8)|mask2;
  mask2=(mask2<<16)|mask2;
//mask2=0x33333333

  mask3=(mask3<<8)|mask3;
  mask3=(mask3<<16)|mask3;
//mask3=0x0f0f0f0f

  mask5=(mask4<<8)|mask4;
//mask5=0x0000ffff

  mask4=(mask4<<16)|mask4;
//mask4=0x00ff00ff

  k=(x&mask1)+((x>>1)&mask1);
  k=(k&mask2)+((k>>2)&mask2);
  k=(k&mask3)+((k>>4)&mask3);
  k=(k&mask4)+((k>>8)&mask4);
  k=(k&mask5)+((k>>16)&mask5);
  return k;
}


//直观写法
int BitCount4(unsigned int n) 
{ 
    n = (n &0x55555555) + ((n >>1) &0x55555555) ; 
    n = (n &0x33333333) + ((n >>2) &0x33333333) ; 
    n = (n &0x0f0f0f0f) + ((n >>4) &0x0f0f0f0f) ; 
    n = (n &0x00ff00ff) + ((n >>8) &0x00ff00ff) ; 
    n = (n &0x0000ffff) + ((n >>16) &0x0000ffff) ; 

    return n ; 
}

本题的要求是统计32位int中1的个数，可以说难度是前5道题中难度最大的，由于不能使用循环，且有操作符个数限制，因此也不能使用暴力的方法，最终我参考了算法-求二进制数中1的个数 - 翰墨小生 - 博客园 (cnblogs.com)中的平行算法。

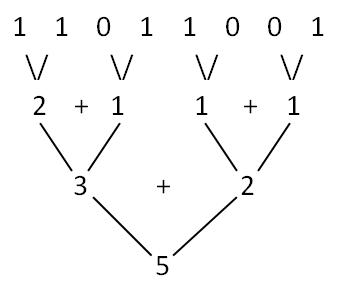
这里构造了五个常数，分别是 0x55555555，0x33333333，0x0f0f0f0f，0x00ff00ff，0x0000ffff，就是分别间隔了1个0,2个0,4个0,8个0和16个0,利用这五个常数就能依次计算出五个值，第一个值每两位的值为 x 的对应的两个位的和（即这两位中 1 的数目），第二个值每四位是第一个值对应的四位中两个两位的和（即原 x 中 1的数目），依次类推最后一个值就是结果了；

5.bang

/* 
 * bang - Compute !x without using !
 *   Examples: bang(3) = 0, bang(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int bang(int x) {
  return ((x>>31)^((x+~0)>>31))&((~x)>>31)&1;
}
//另一种实现
int bang(int x) {
  x=(x>>16)|x;
  x=(x>>8)|x;
  x=(x>>4)|x;
  x=(x>>2)|x;
  x=(x>>1)|x;
  return ~x&0x1;
}

本题要求使用不使用！来实现！。我在实现时发现了一个规律，对于x和x-1只有两种情况两个数的第31位是相反的，一是x=0,x-1=0xffffffff,二是x=0x80000000,x-1=0x7fffffff,因此利用异或把这种情况再特判要求x的31位为0即可满足条件。

另一种实现是使用了折叠法，把32个位上的1通过折叠的方式聚合到0位上，即只要有一个位为1，最终得到的就是0x1，否则为0，之后再对其进行处理，该方法更加巧妙。

2.补码

6.tmin

/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return (1<<31);
}

最高位为1，其他位为0为最小值。

7.fitsBits

/* 
 * fitsBits - return 1 if x can be represented as an 
 *  n-bit, two's complement integer.
 *   1 <= n <= 32
 *   Examples: fitsBits(5,3) = 0, fitsBits(-4,3) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 2
 */
int fitsBits(int x, int n) {
  int mask=x>>31;
//  int check=x>>n;
  int check=x>>(n+~0);
  return (!check&!mask)|(!(check+1)&mask);
}

本题为判断用n位能否用补码的形式表示一个x的数字，本题的解法是分情况讨论，分别为x>=0和x<0两种情况，将x向右移n-1位，判断其是否为0（负数的时候为-1），得到最终结果。

8.divpwr2

/* 
 * divpwr2 - Compute x/(2^n), for 0 <= n <= 30
 *  Round toward zero
 *   Examples: divpwr2(15,1) = 7, divpwr2(-33,4) = -2
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 2
 */
int divpwr2(int x, int n) {
//当x为负数时，才增加偏正因子
    int mask=!(x>>31)+~0;
//    return ((x>>n)&~mask)|(((x+(1<<n)+~0)>>n)&mask);
    return (x+(((1<<n)+~0)&mask))>>n;
}

这题计算 x/(2^n) ，注意不能直接右移，直接右移是向下舍入的，题目要求是向零舍入，也就是正数向下舍入，负数向上舍入，这里参照 CS:APP 书上的做法，给负数加上一个偏正的因子 (0x1<<n)+~0) ，判断负数直接看符号位。

9.negate

/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return ~x+1;
}

利用-x=~x+1

10.isPositive

/* 
 * isPositive - return 1 if x > 0, return 0 otherwise 
 *   Example: isPositive(-1) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 8
 *   Rating: 3
 */
int isPositive(int x) {
  return !((x>>31)|!x);
}

判断是否x>0,结合符号位，特判x=0的情况即可。

11.isLessOrEqual

/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  int x1=x>>31;
  int y1=y>>31;
  int z=x+~y+1;
  int flag=z>>31|!z;
  return ((x1&!y1)|(x1&y1&flag)|(!x1&!y1&flag))&1;
}

对于x<=y,可以分几种情况讨论。

x<0,y>0时显然成立
x<0,y<0,x-y<=0时成立，且x-y不会出现溢出
x>0,y>0,x-y<=0时成立，且x-y不会出现溢出

因此分三种情况讨论结合即可，x1,y1即是对正负性的判断

12.ilog2

/*
 * ilog2 - return floor(log base 2 of x), where x > 0
 *   Example: ilog2(16) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 90
 *   Rating: 4
 */
int ilog2(int x) {
  int flag1=!(x>>16);
  int flag2=0,flag3=0,flag4=0,flag5=0;
//x>>16>0时，x=x>>16，否则x=x，下方同理
  x=(x>>16&(flag1+~0))|(x&(!flag1+~0));
  flag2=!(x>>8);
  x=(x>>8&(flag2+~0))|(x&(!flag2+~0));
  flag3=!(x>>4);
  x=(x>>4&(flag3+~0))|(x&(!flag3+~0));
  flag4=!(x>>2);
  x=(x>>2&(flag4+~0))|(x&(!flag4+~0));
  flag5=!(x>>1);
  x=(x>>1&(flag5+~0))|(x&(!flag5+~0));
  return !flag5+(!flag4<<1)+(!flag3<<2)+(!flag2<<3)+(!flag1<<4);
}

上方的flag1-5得到的是x的最高位对应的2进制表示中是否包含16,8,4,2,1的底数，因为其对数可表示成16*a+8*b+4*c+2*d+e的形式，最终拼接起来即为最终结果，注意的是每一步对x进行了条件判断的赋值。

3.浮点数

以下三题关于浮点数，可以自由使用操作符和分支语句

13.float_neg

/* 
 * float_neg - Return bit-level equivalent of expression -f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representations of
 *   single-precision floating point values.
 *   When argument is NaN, return argument.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 10
 *   Rating: 2
 */
unsigned float_neg(unsigned uf) {
  if((uf&0x7fffff)&&(((uf>>23)&0xff)==0xff)){
    return uf;
  }else{
    return uf^0x80000000;
 }
}

本题计算-f，即参数的负数，注意特判NaN的情况。

14.float_i2f

/* 
 * float_i2f - Return bit-level equivalent of expression (float) x
 *   Result is returned as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point values.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned float_i2f(int x) {
  int sign=x&0x80000000;
  int xt=x;
  int big=-1,index=0;
  int exp=0,frac=0,cp1=0,cp2=0;
//特判
  if(x==0)
    return 0;
  if(x==0x80000000)
    return 0xcf000000;
//根据符号位，取反  
  if(sign){
   x=-x;
  }
//  int big=oilog2(x&0xffffffff);
  xt=0x7fffffff&x;
  while(xt){
   xt=xt>>1;
   big=big+1;
  }
  exp=127+big;
  index=big-23;
  if(index>0){
   frac=(x>>index);
   cp1=1<<(big-24);
   cp2=x&((cp1<<1)-1);
   if(cp2>cp1){
     frac=frac+1;
   }else if(cp2==cp1){
     if(frac&1){
       frac=frac+1;
     }
   }
  } else{
   frac=(x<<-index);
  }

  if(frac==0x1000000){
     exp=exp+1;
  } 
  return (exp<<23)|sign|(frac&0x7fffff);
}

本题为将整型数转化为浮点数格式，可以说是本lab里难度最大的题目，具有很多坑点，解读参考博客的解法。

整体思路就是依次计算符号位，阶码值和小数字段，符号位可以直接移位提取，阶码值就是除了符号位外最高位的位数减 1 再加上偏差 127，小数字段可以移位（负数可以化为正数操作）获得，但这问题没这么简单，有很多坑点：

特殊值 0 化为浮点数后是非规格化的，单独考虑；
特殊值 0x80000000 是 2 的整数倍，小数部分用移位的话因为舍入问题会溢出，单独考虑；
要仔细考虑移位过程，左移还是右移能得到 23 位的小数部分，这里实际上是需要进行分类讨论，左移直接执行即可，右移由于涉及到舍入，所以需要进行一些判断；
注意舍入问题，这里需要仔仔细细地考虑清楚，**默认使用向偶数舍入，就是舍去部分小于中间值舍弃，大于中间值进位，为中间值如 100 就向偶数舍入：就是看前一位，进位或舍弃总使得前一位为 0。 **舍入的知识可以参考(29条消息) 浮点数向偶数舍入的问题_南京大学的CS渣-CSDN博客_向偶数舍入
最后就是操作数目限制在 30 位，这个需要对写完的代码进行一步步精简，我最终的实现正好是30个操作符。

15.float_twice

/* 
 * float_twice - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned float_twice(unsigned uf) {
  int tmp=uf;
  int sign=((uf>>31)<<31); /* 0x80000000 or 0x0 */
  int exp=uf&0x7f800000;
  int f=uf&0x7fffff;
  tmp=tmp&0x7fffffff; /* remove sign */
  if((tmp>>23)==0x0){
    tmp=tmp<<1|sign;
    return tmp;
  } else if((tmp>>23)==0xff){
    return uf;
  }  else{
    if((exp>>23)+1==0xff){
      return sign|0x7f800000;
    }else{
      return sign|(((exp>>23)+1)<<23)|f;
    }
  }
  return tmp;
}

本题为求参数的2倍，对于无穷大和NAN的情况直接返回，其他情况需要分规格化和非规格化两种情况讨论。

对于规格化的情况，在阶码值上+1，但是对于溢出的时候需要返回无穷大
对于非规格化情况，将除符号位的数字左移一位即可，因为这时阶码值为 0 ,两倍就相当于小数字段左移一位，不用担心溢出的情况，溢出时阶码值加 1,小数字段左移一位，相当于整体左移了。（这里可以感叹一下浮点数编码设计的巧妙！）

总结

本lab虽然面向的知识比较基础，但是难度并不小，需要在写码的过程中，不断琢磨各种精妙和可靠的实现（例如使用|和&来实现分类讨论），花费了数天的时间完成（包括搭建和熟悉环境）。

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

数学建模美赛（一）：拟合与插值下一篇

CSAPP(一):Data Lab笔记

前言：